分类问题与回归问题的损失函数
分类问题损失函数
多分类交叉熵损失Softmax

其中:
1.y 是样本 x 属于某一个类别的真实概率[用0,1表示]
2.而 f(x) 是样本属于某一类别的预测分数
3.S 是 softmax 激活函数,将属于某一类别的预测分数转换成概率
4.L 用来衡量真实值 y 和预测值 f(x) 之间差异性的损失结果
公式鼓励模型对正确类别给出高概率,对错误类别给出低概率。当预测完全正确时,损失为0;当预测错误时,损失会变大。
二分类损失----对数似然损失(Log Loss)
在处理二分类任务时,我们不再使用softmax激活函数,而是使用sigmoid激活函数,那损失函数也相应的进行调整,使用二分类的交叉熵损失函数:

其中:
- y 是样本x属于某一个类别的真实概率
- 而y^是样本属于某一类别的预测概率
- L用来衡量真实值y与预测值y^之间差异性的损失结果。
焦点损失 (Focal Loss)
它是交叉熵损失的改进版本 , 由何恺明等人在2017年提出,最初用于解决目标检测中的前景-背景类别不平衡问题。
FL(pt) = -α(1-pt)^γ * log(pt)
其中:
pt 是模型预测的概率
α 是平衡因子(用于平衡正负样本)
γ 是聚焦参数(用于调节简单样本的权重)
原理:
- 焦点损失通过降低容易分类的样本(高置信度预测)的权重,使模型更关注难以分类的样本。
- (1-pt)^γ项使得易分样本(pt接近1)的损失贡献较小,而难分样本的损失贡献较大。
优点:
- 有效解决类别不平衡问题,特别是在极度不平衡的情况下。
- 自动降低简单样本的权重,让模型更专注于难样本。
- 不需要进行硬性的样本挖掘。
应用:
- 目标检测
- 图像分类
- 其他存在类别不平衡的分类问题
参数调节:
- γ 通常设置为0到5之间。γ 越大,对易分样本的抑制越强。
- α 可以设置为类别频率的倒数,也可以通过交叉验证调整。
回归问题损失函数
又称loss function/cost function 目标函数 成本函数
以下公式中, h(x^i )为拟合函数,y^i 为真实值
最小二乘损失计算:

均方误差 (Mean-Square Error, MSE) 又叫L2损失

平均绝对误差 (Mean Absolute Error , MAE) 又叫L1损失

注MSE与MAE既能在模型训练阶段作为损失函数求解拟合函数最优解 , 又可作为模型评估阶段, 衡量已有模型误差大小
smooth L1 lose
平滑后的L1lose,分段函数

其中:𝑥 = f(x) − y 为真实值和预测值的差值。
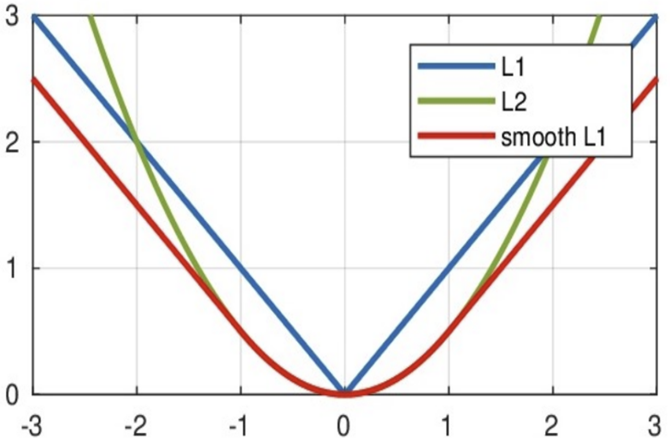
从下图中可以看出,该函数实际上就是一个分段函数
- 在[-1,1]之间实际上就是L2损失,这样解决了L1的不光滑问题
- 在[-1,1]区间外,实际上就是L1损失,这样就解决了离群点梯度爆炸的问题
分类问题与回归问题的损失函数
https://linxkon.github.io/分类问题与回归问题的损失函数.html