神经网络简明教程
本篇文章试图使用最简洁易懂的文字对一个典型神经网络做一个较为完整的介绍。力求读者在读完本篇文章后对神经网络能有一个清晰且全面的认识。
任务描述
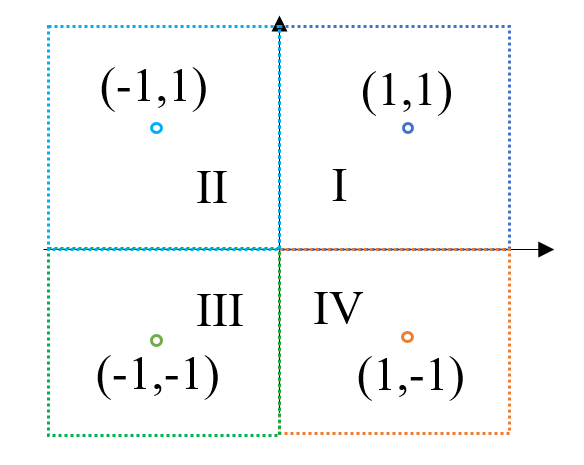
如下图,我们已知四个数据点(1,1)(-1,1)(-1,-1)(1,-1),这四个点分别对应I~IV象限,如果这时候给我们一个新的坐标点(比如(2,2)),那么它应该属于哪个象限呢?(没错,当然是第I象限,但我们的任务是要让机器知道)
“分类”是神经网络的一大应用,我们使用神经网络完成这个分类任务。
两层神经网络
这里我们构建一个两层神经网络,理论上两层神经网络已经可以拟合任意函数。这个神经网络的结构如下图:
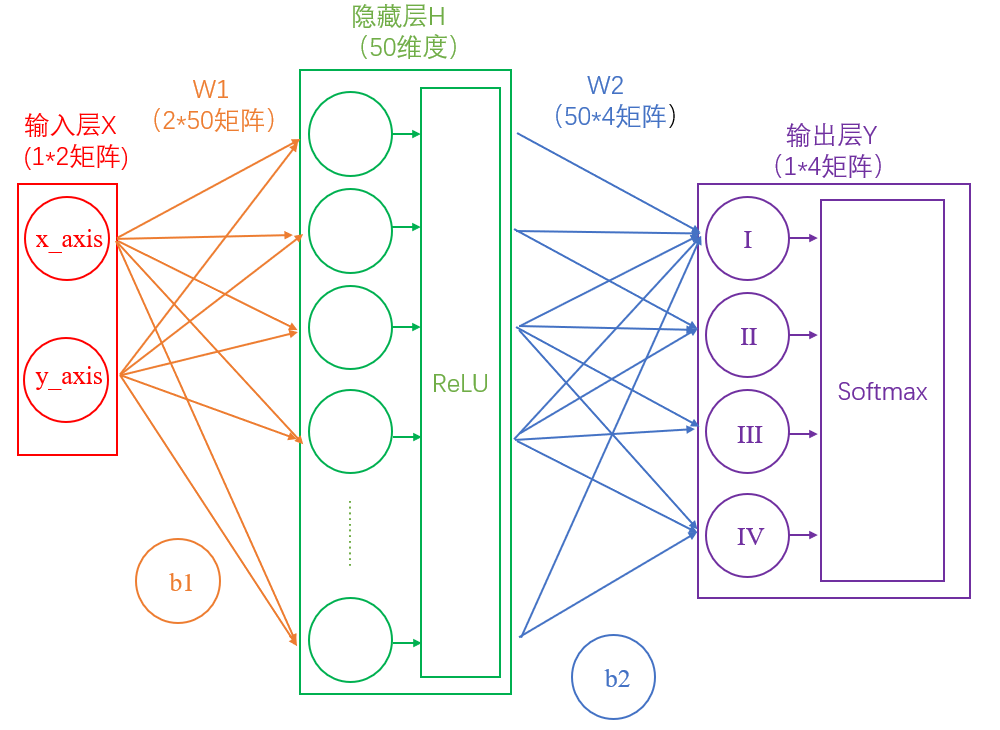
是不是觉得有点复杂,没关系,我们一步步看,其实很容易理解。
1.简化的两层神经网络分析
首先去掉图1中一些难懂的东西,如下图(请仔细看一下图中的标注):
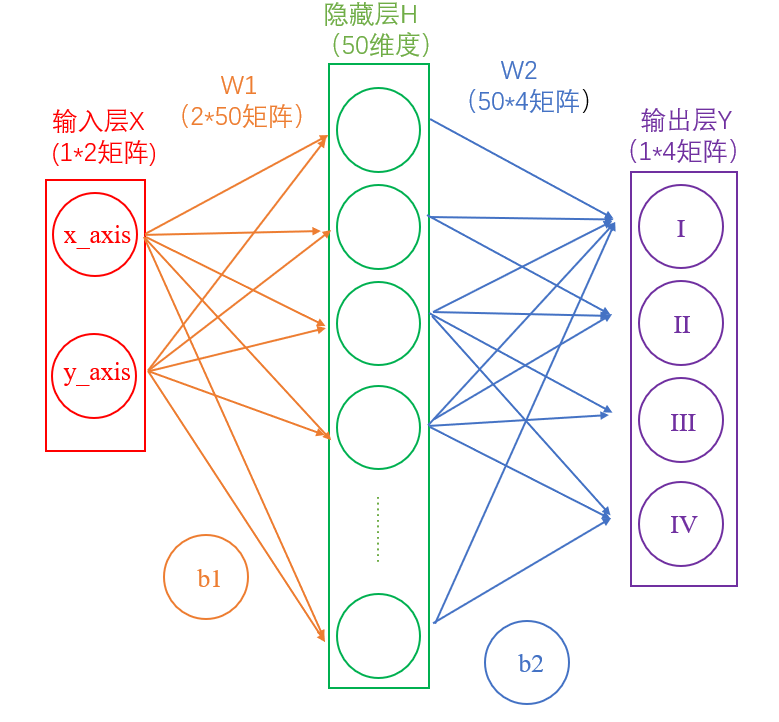
1.1.输入层
在我们的例子中,输入层是坐标值,例如(1,1),这是一个包含两个元素的数组,也可以看作是一个12的矩阵。输入层的元素维度与输入量的特征息息相关,如果输入的是一张3232像素的灰度图像,那么输入层的维度就是32*32。
1.2.从输入层到隐藏层
连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单,就是矩阵运算:

如果你学过线性代数,对这个式子一定不陌生。如上图中所示,在设定隐藏层为50维(也可以理解成50个神经元)之后,矩阵H的大小为(1*50)的矩阵。
1.3.从隐藏层到输出层
连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:

1.4.分析
通过上述两个线性方程的计算,我们就能得到最终的输出Y了,但是如果你还对线性代数的计算有印象的话,应该会知道:*一系列线性方程的运算最终都可以用一个线性方程表示*。也就是说,上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样,就算网络深度加到100层,也依然是这样。这样的话神经网络就失去了意义。
所以这里要对网络注入灵魂:激活层。
2.激活层
简而言之,激活层是为矩阵运算的结果添加非线性的。常用的激活函数有三种,分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到,其实它们的形式都很简单,如下图:
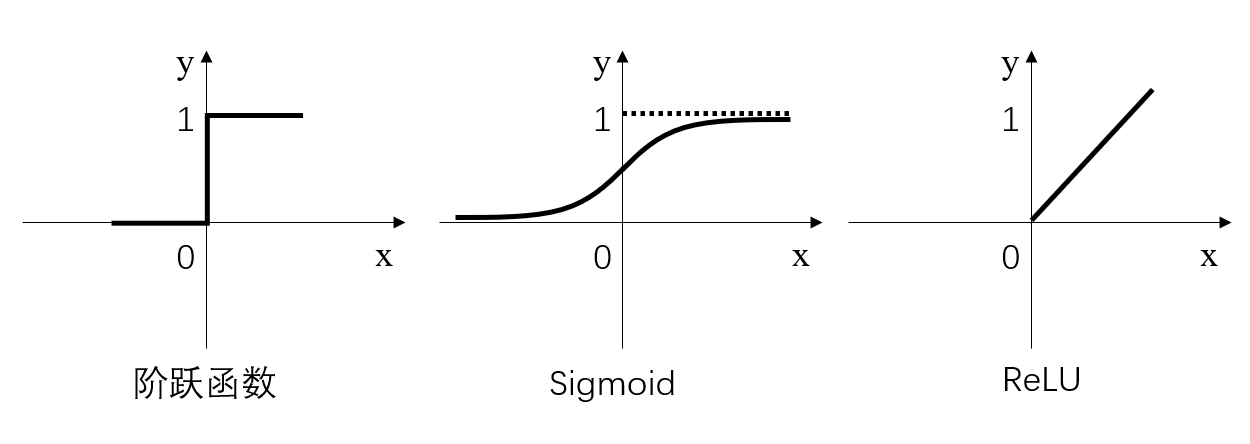
图3.三种常用的激活函数
阶跃函数:当输入小于等于0时,输出0;当输入大于0时,输出1。
Sigmoid:当输入趋近于正无穷/负无穷时,输出无限接近于1/0。
ReLU:当输入小于0时,输出0;当输入大于0时,输出等于输入。
其中,阶跃函数输出值是跳变的,且只有二值,较少使用;Sigmoid函数在当x的绝对值较大时,曲线的斜率变化很小(梯度消失),并且计算较复杂;ReLU是当前较为常用的激活函数。
激活函数具体是怎么计算的呢?
假如经过公式H=X*W1+b1计算得到的H值为:(1,-2,3,-4,7...),那么经过阶跃函数激活层后就会变为(1,0,1,0,1...),经过ReLU激活层之后会变为(1,0,3,0,7...)。
需要注意的是,每个隐藏层计算(矩阵线性运算)之后,都需要加一层激活层,要不然该层线性计算是没有意义的。
此时的神经网络变成了如下图所示的形式:
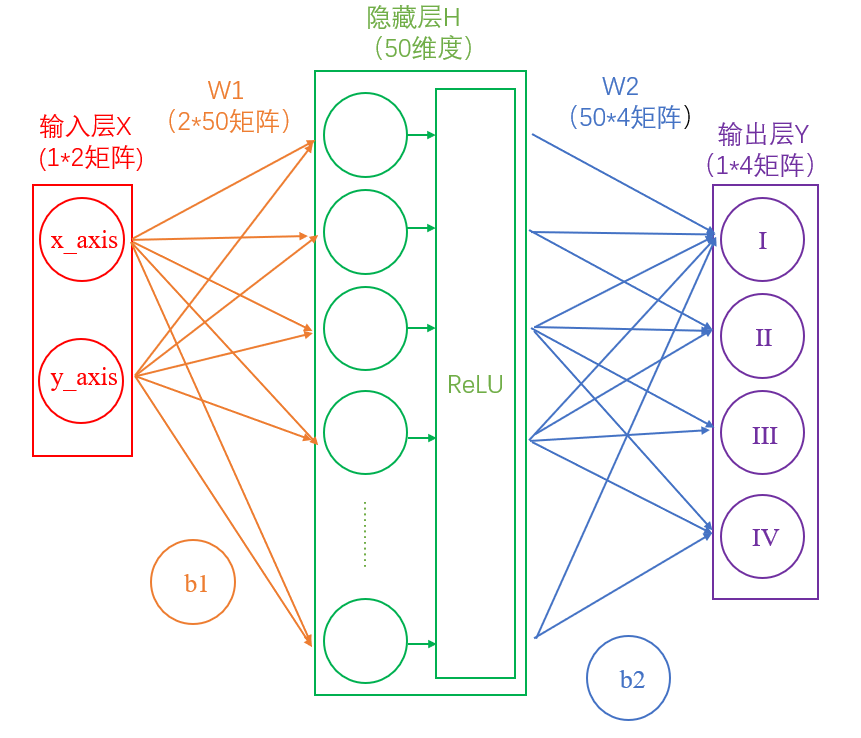
图4.加上激活层的两层神经网络
神经网络是分为“训练”和“使用”两个步骤的。如果是在“使用”的步骤,图4就已经完成整个过程了,在求得的Y(大小为1*4)矩阵中,数值最大的就代表着当前分类。
但是对于用于“训练”的网络,图4还远远不够。起码当前的输出Y,还不够“漂亮”。
3.输出的正规化
在图4中,输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为概率,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。
具体是怎么计算的呢?
计算公式如下:
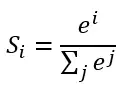
简单来说分三步进行:(1)以e为底对所有元素求指数幂;(2)将所有指数幂求和;(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成如下图所示:

4.如何衡量输出的好坏
通过Softmax层之后,我们得到了I,II,III和IV这四个类别分别对应的概率,但是要注意,这是神经网络计算得到的概率值结果,而非真实的情况。
比如,Softmax输出的结果是(90%,5%,3%,2%),真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类,但是与真实结果之间是有差距的,一个优秀的网络对结果的预测要无限接近于100%,为此,我们需要将Softmax输出结果的好坏程度做一个“量化”。
一种直观的解决方法,是用1减去Softmax输出的概率,比如1-90%=0.1。不过更为常用且巧妙的方法是,求对数的负数。
还是用90%举例,对数的负数就是:-log0.9=0.046
可以想见,概率越接近100%,该计算结果值越接近于0,说明结果越准确,该输出叫做“交叉熵损失(Cross Entropy Error)”。
我们训练神经网络的目的,就是尽可能地减少这个“交叉熵损失”。
此时的网络如下图:
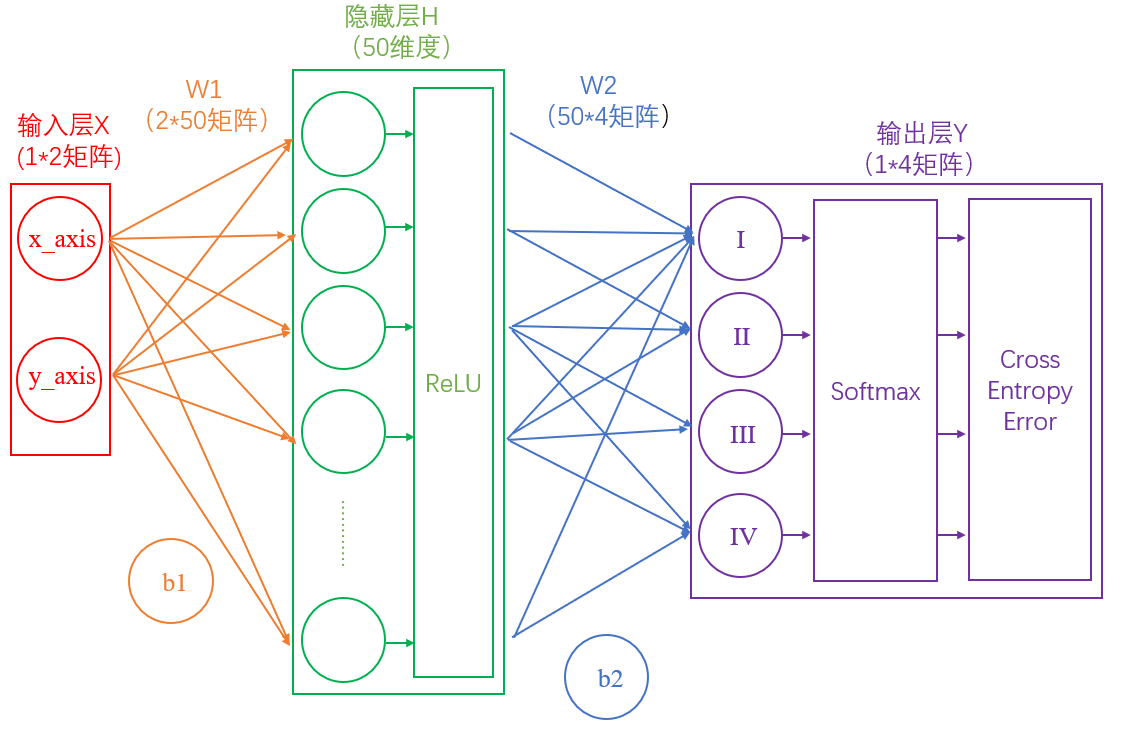
5.反向传播与参数优化
上边的1~4节,讲述了神经网络的正向传播过程。一句话复习一下:神经网络的传播都是形如Y=WX+b的矩阵运算;为了给矩阵运算加入非线性,需要在隐藏层中加入激活层;输出层结果需要经过Softmax层处理为概率值,并通过交叉熵损失来量化当前网络的优劣。
算出交叉熵损失后,就要开始反向传播了。其实反向传播就是一个参数优化的过程,优化对象就是网络中的所有W和b(因为其他所有参数都是确定的)。
神经网络的神奇之处,就在于它可以自动做W和b的优化,在深度学习中,参数的数量有时会上亿,不过其优化的原理和我们这个两层神经网络是一样的。
这里举一个形象的例子描述一下这个参数优化的原理和过程:
假设我们操纵着一个球型机器行走在沙漠中

我们在机器中操纵着四个旋钮,分别叫做W1,b1,W2,b2。当我们旋转其中的某个旋钮时,球形机器会发生移动,但是旋转旋钮大小和机器运动方向之间的对应关系是不知道的。而我们的目的就是走到沙漠的最低点。

此时我们该怎么办?只能挨个试喽。
如果增大W1后,球向上走了,那就减小W1。
如果增大b1后,球向下走了,那就继续增大b1。
如果增大W2后,球向下走了一大截,那就多增大些W2。
。。。
这就是进行参数优化的形象解释(有没有想到求导?),这个方法叫做梯度下降法。
当我们的球形机器走到最低点时,也就代表着我们的交叉熵损失达到最小(接近于0)。
关于反向传播,还有许多可以讲的,但是因为内容较多,就放在下一篇文章中说吧。不过上述例子对于理解神经网络参数优化的过程,还是很有帮助的。
6.迭代
神经网络需要反复迭代。
如上述例子中,第一次计算得到的概率是90%,交叉熵损失值是0.046;将该损失值反向传播,使W1,b1,W2,b2做相应微调;再做第二次运算,此时的概率可能就会提高到92%,相应地,损失值也会下降,然后再反向传播损失值,微调参数W1,b1,W2,b2。依次类推,损失值越来越小,直到我们满意为止。
此时我们就得到了理想的W1,b1,W2,b2。
此时如果将任意一组坐标作为输入,利用图4或图5的流程,就能得到分类结果。
此时,我们一个简单的基本神经网络模型就构建完成啦~