激活函数简明教程
一、什么是激活函数?
在接触到深度学习(Deep Learning)后,特别是神经网络中,我们会发现在每一层的神经网络输出后都会使用一个函数(比如sigmoid,tanh,Relu等等)对结果进行运算,这个函数就是激活函数(Activation Function)。那么为什么需要添加激活函数呢?如果不添加又会产生什么问题呢?
首先,我们知道神经网络模拟了人类神经元的工作机理,激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。在神经元中,输入的input经过一系列加权求和后作用于另一个函数,这个函数就是这里的激活函数。类似于人类大脑中基于神经元的模型,激活函数最终决定了是否传递信号以及要发射给下一个神经元的内容。在人工神经网络中,一个节点的激活函数定义了该节点在给定的输入或输入集合下的输出。标准的计算机芯片电路可以看作是根据输入得到开(1)或关(0)输出的数字电路激活函数。
激活函数可以分为线性激活函数(线性方程控制输入到输出的映射,如f(x)=x等)以及非线性激活函数(非线性方程控制输入到输出的映射,比如Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等)
这里来解释下为什么要使用激活函数?
因为神经网络中每一层的输入输出都是一个线性求和的过程,下一层的输出只是承接了上一层输入函数的线性变换,所以如果没有激活函数,那么无论你构造的神经网络多么复杂,有多少层,最后的输出都是输入的线性组合,纯粹的线性组合并不能够解决更为复杂的问题。而引入激活函数之后,我们会发现常见的激活函数都是非线性的,因此也会给神经元引入非线性元素,使得神经网络可以逼近其他的任何非线性函数,这样可以使得神经网络应用到更多非线性模型中。
在神经网络中,神经元的工作原理可以用下图进行表示:
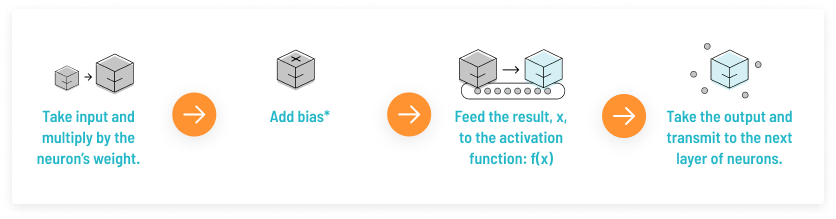
上述过程的数学可视化过程如下图所示:
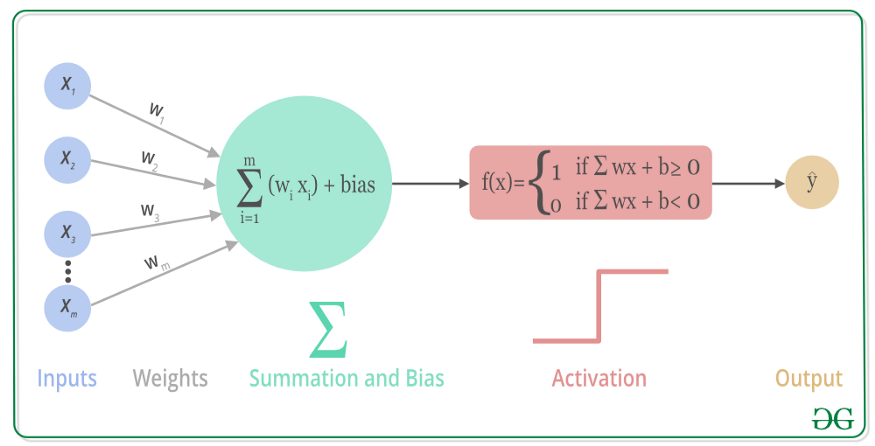
一般来说,在神经元中,激活函数是很重要的一部分,为了增强网络的表示能力和学习能力,神经网络的激活函数都是非线性的,通常具有以下几点性质:
- 连续并可导(允许少数点上不可导),可导的激活函数可以直接利用数值优化的方法来学习网络参数;
- 激活函数及其导数要尽可能简单一些,太复杂不利于提高网络计算率;
- 激活函数的导函数值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性。
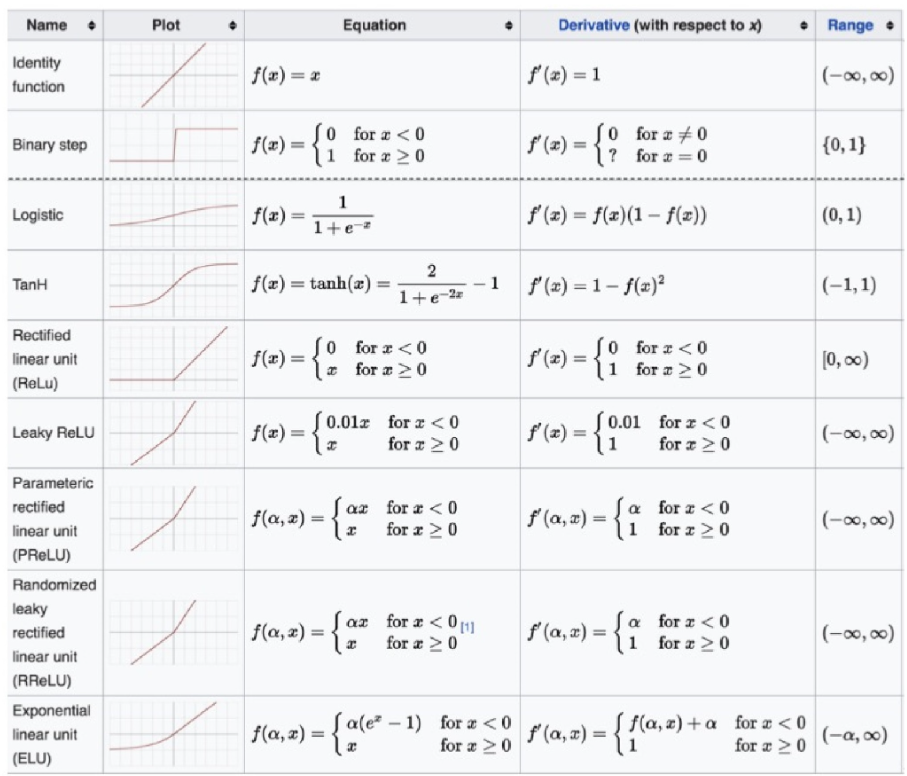
二、常见的激活函数
1. Sigmoid函数
Sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。sigmoid是一个十分常见的激活函数,函数的表达式如下:
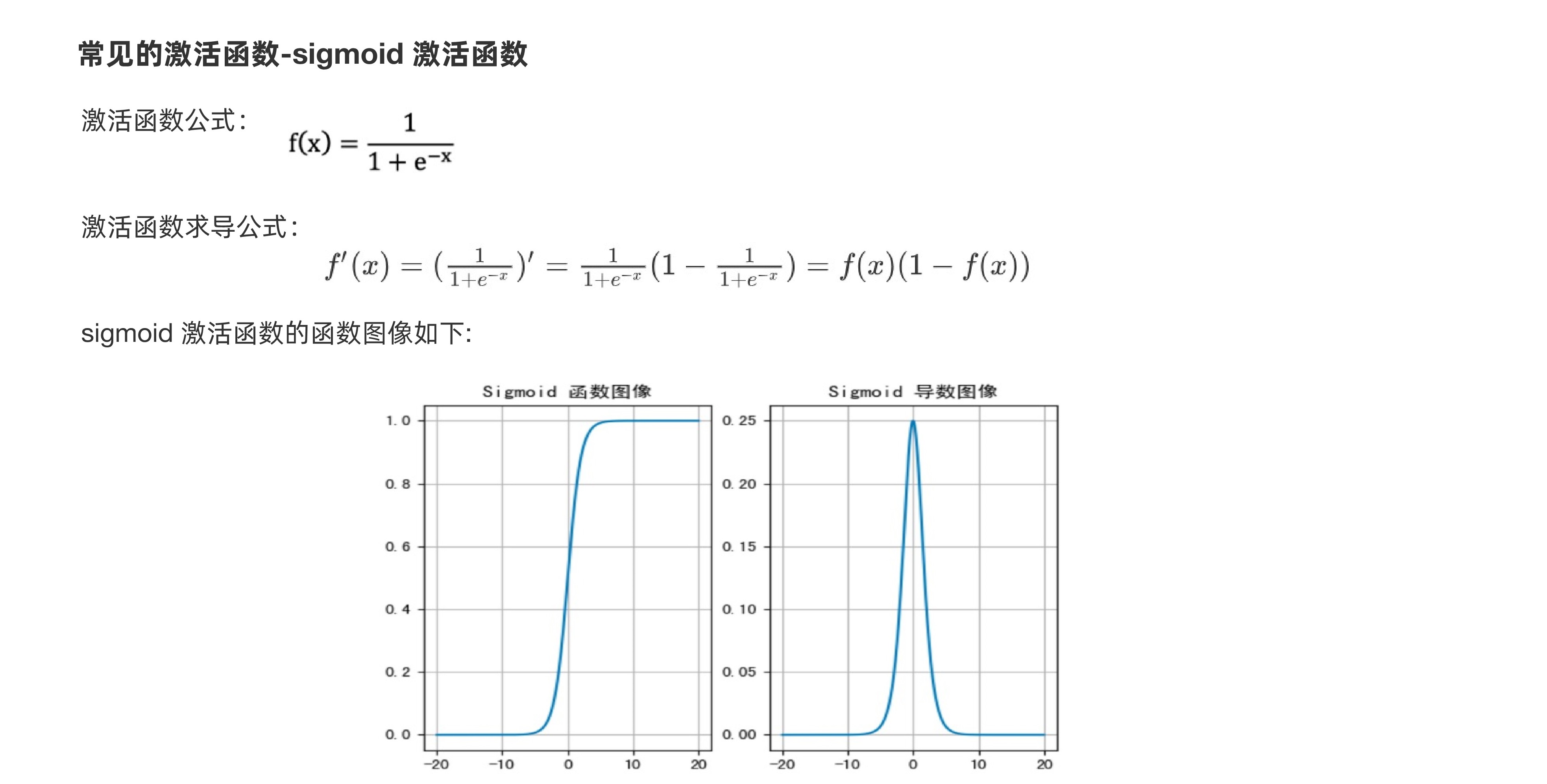
在什么情况下适合使用 Sigmoid 激活函数呢?
- Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1,因此它对每个神经元的输出进行了归一化;
- 用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1,因此 Sigmoid 函数非常合适;
- 梯度平滑,避免「跳跃」的输出值;
- 函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率;
- 明确的预测,即非常接近 1 或 0。
Sigmoid 激活函数存在的不足:
- 梯度消失:注意:Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦,也就是说,Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时,输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此,这些神经元的权重不会更新。此外,与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此,想象一下,如果一个大型神经网络包含 Sigmoid 神经元,而其中很多个都处于饱和状态,那么该网络无法执行反向传播。
- 不以零为中心:Sigmoid 输出不以零为中心的,,输出恒大于0,非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(Bias Shift),并进一步使得梯度下降的收敛速度变慢。
- 计算成本高昂:exp() 函数与其他非线性激活函数相比,计算成本高昂,计算机运行起来速度较慢。
2. Tanh/双曲正切激活函数
Tanh 激活函数又叫作双曲正切激活函数(hyperbolic tangent activation function)。与 Sigmoid 函数类似,Tanh 函数也使用真值,但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同,Tanh 函数的输出以零为中心,因为区间在-1 到 1 之间。
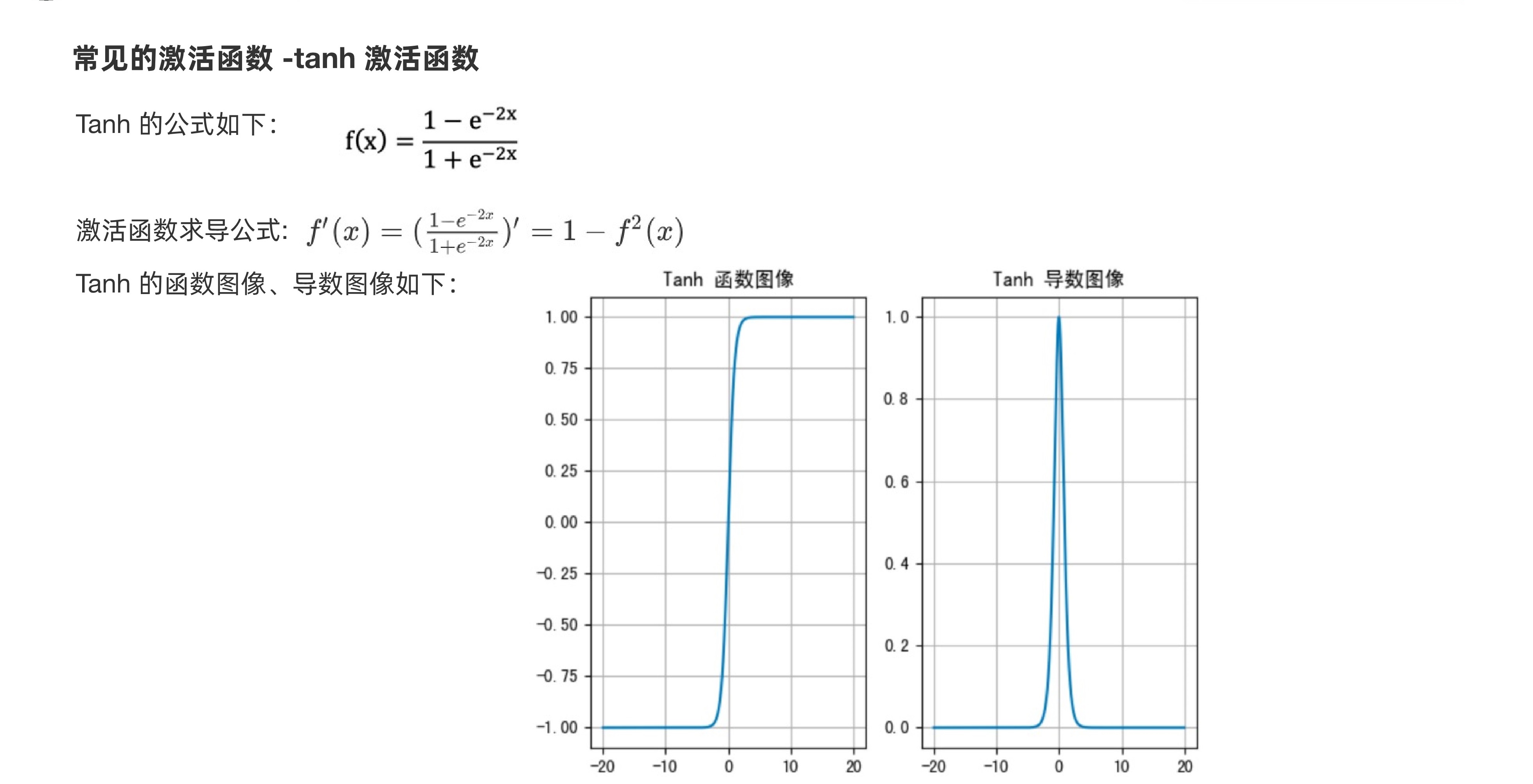
我们可以发现Tanh 函数可以看作放大并平移的Logistic 函数,其值域是(−1, 1)。Tanh与sigmoid的关系如下:
𝑡𝑎𝑛ℎ(𝑥)=2𝑠𝑖𝑔𝑚𝑜𝑖𝑑(2𝑥)−1
tanh 激活函数的图像也是 S 形,作为一个双曲正切函数,tanh 函数和 sigmoid 函数的曲线相对相似。但是它比 sigmoid 函数更有一些优势。 你可以将 Tanh 函数想象成两个 Sigmoid 函数放在一起。在实践中,Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值,零输入值的映射接近零,正数输入被当作正值:
- 当输入较大或较小时,输出几乎是平滑的并且梯度较小,这不利于权重更新。二者的区别在于输出间隔,tanh 的输出间隔为 1,并且整个函数以 0 为中心,比 sigmoid 函数更好;
- 在 tanh 图中,负输入将被强映射为负,而零输入被映射为接近零。
tanh存在的不足:
- 与sigmoid类似,Tanh 函数也会有梯度消失的问题,因此在饱和时(x很大或很小时)也会「杀死」梯度。
注意:在一般的二元分类问题中,tanh 函数用于隐藏层,而 sigmoid 函数用于输出层,但这并不是固定的,需要根据特定问题进行调整。
3. ReLU激活函数
ReLU函数又称为修正线性单元(Rectified Linear Unit),是一种分段线性函数,其弥补了sigmoid函数以及tanh函数的梯度消失问题,在目前的深度神经网络中被广泛使用。ReLU函数本质上是一个斜坡(ramp)函数,公式及函数图像如下:
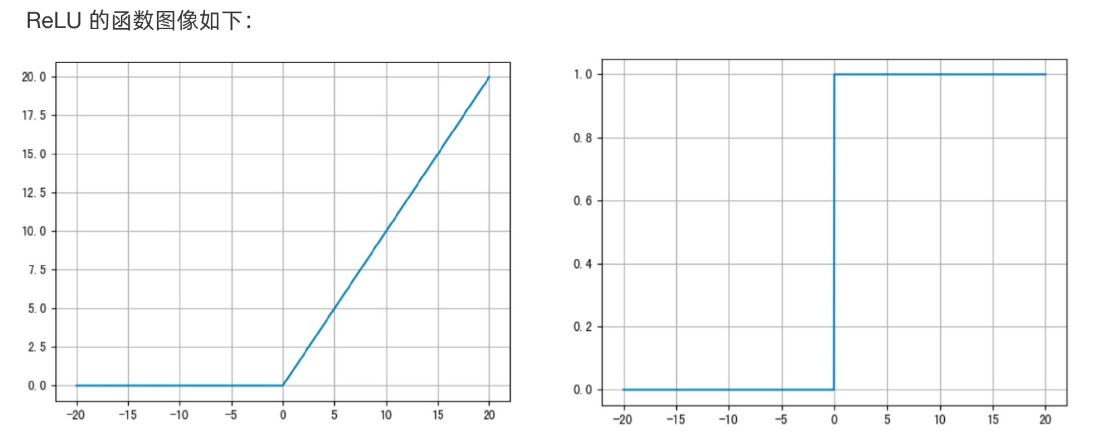
ReLU 函数是深度学习中较为流行的一种激活函数,相比于 sigmoid 函数和 tanh 函数,它具有如下优点:
- 当输入为正时,导数为1,一定程度上改善了梯度消失问题,加速梯度下降的收敛速度;
- 计算速度快得多。ReLU 函数中只存在线性关系,因此它的计算速度比 sigmoid 和 tanh 更快。
- 被认为具有生物学合理性(Biological Plausibility),比如单侧抑制、宽兴奋边界(即兴奋程度可以非常高)
ReLU函数的不足:
- Dead ReLU 问题。当输入为负时,ReLU 完全失效,在正向传播过程中,这不是问题。有些区域很敏感,有些则不敏感。但是在反向传播过程中,如果输入负数,则梯度将完全为零;
【Dead ReLU问题】ReLU神经元在训练时比较容易“死亡”。在训练时,如果参数在一次不恰当的更新后,第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远不能被激活。这种现象称为死亡ReLU问题,并且也有可能会发生在其他隐藏层。
- 不以零为中心:和 Sigmoid 激活函数类似,ReLU 函数的输出不以零为中心,ReLU 函数的输出为 0 或正数,给后一层的神经网络引入偏置偏移,会影响梯度下降的效率。
4. Leaky ReLU
为了解决 ReLU 激活函数中的梯度消失问题,当 x < 0 时,我们使用 Leaky ReLU——该函数试图修复 dead ReLU 问题。下面我们就来详细了解 Leaky ReLU。
函数表达式以及图像如下:
LeakyReLU (𝑥)={𝑥 if 𝑥>0𝛾𝑥 if 𝑥≤0=max(0,𝑥)+𝛾min(0,𝑥),
其中 𝛾 是一个很小的数,如0.1,0.01等等。这里,令 𝛾=0.1 进行展示:
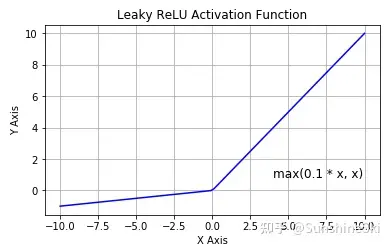
对于 𝛾<1 ,Leaky ReLU也可以写作:
LeakyReLU( 𝑥)=max(𝑥,𝛾𝑥)
相当于是一个比较简单的Maxout单元(Maxout函数会在下面讲解)
为什么使用Leaky ReLU会比ReLU效果要好呢?
- Leaky ReLU 通过把 x 的非常小的线性分量给予负输入(0.01x)来调整负值的零梯度(zero gradients)问题,当 x < 0 时,它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题,
- leak 有助于扩大 ReLU 函数的范围,通常 a 的值为 0.01 左右;
- Leaky ReLU 的函数范围是(负无穷到正无穷)
尽管Leaky ReLU具备 ReLU 激活函数的所有特征(如计算高效、快速收敛、在正区域内不会饱和),但并不能完全证明在实际操作中Leaky ReLU 总是比 ReLU 更好。
5. Parametric ReLU激活函数
Leaky ReLU 是在ReLU的基础上针对存在的问题进行的扩展。除此以外也可以从其他角度进行扩展,不让 x 乘常数项,而是让 x 乘超参数,这看起来比 Leaky ReLU 效果要好,这一种扩展就是 Parametric ReLU,即为带参数的ReLU函数。
函数表达式为:
PReLU𝑖(𝑥)={𝑥 if 𝑥>0𝛾𝑖𝑥 if 𝑥≤0=max(0,𝑥)+𝛾𝑖min(0,𝑥),
其中 𝛾𝑖 是超参数,对应了 𝑥≤0 时函数的斜率。这里引入了一个随机的超参数,它可以被学习,可以对它进行反向传播。不同神经元可以有不同的参数,其中的i对应了第i个神经元,这使神经元能够选择负区域最好的梯度,有了这种能力,它们可以变成 ReLU 或 Leaky ReLU。
如果 𝛾𝑖=0 ,那么PReLU 就退化为ReLU;
如果 𝛾𝑖 为一个很小的常数,则PReLU 可以看作Leaky ReLU;
PReLU 可以允许不同神经元具有不同的参数,也可以一组神经元共享一个参数。
在很多情况下,最好使用 ReLU,但是你可以使用 Leaky ReLU 或 Parametric ReLU 进行实践,看看哪一种方式是否更适合你的问题。
6. ELU激活函数
ELU(Exponential Linear Unit) 的提出同样也是针对解决 ReLU负数部分存在的问题,由Djork等人提出,被证实有较高的噪声鲁棒性。ELU激活函数对 𝑥 小于零的情况采用类似指数计算的方式进行输出。与 ReLU 相比,ELU 有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度。 函数表达式为
g(𝑥)=ELU(𝑥)={𝑥,𝑥>0𝛼(e𝑥−1),𝑥⩽0
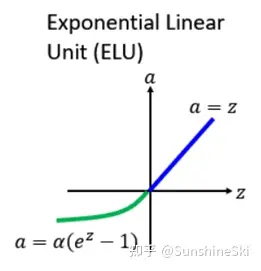
显然,ELU 具有 ReLU 的所有优点,并且:
- 没有 Dead ReLU 问题,输出的平均值接近 0,以 0 为中心;
- ELU 通过减少偏置偏移的影响,使正常梯度更接近于单位自然梯度,从而使均值向零加速学习;
- ELU 在较小的输入下会饱和至负值,从而减少前向传播的变异和信息。
一个小问题是它的计算强度更高,计算量较大。与 Leaky ReLU 类似,尽管理论上比 ReLU 要好,但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。
7. SeLU激活函数
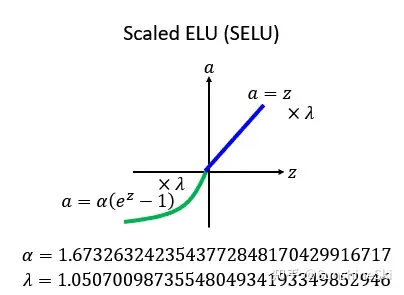
Self-Normalizing Neural Networks(SNNs)论文中SNN基于缩放的指数线性单位“ SELU”,可诱导自标准化属性(例如方差稳定化),从而避免了梯度的爆炸和消失。 SELU函数是给ELU函数乘上系数 𝜆 , 即 𝑆𝐸𝐿𝑈(𝑥)=𝜆⋅𝐸𝐿𝑈(𝑥)
𝑓(𝑥)=𝜆{𝛼(𝑒𝑥−1)𝑥≤0𝑥𝑥>0
通过论文中大量的证明,作者给出了 𝜆 和 𝛼 的值:
SELU函数的特点是:
- 它的值有正有负:在整个ReLU的family里里面,除了一开始最原始的ReLU以外都有负值,该函数也贯彻了这个特性;
- 有Saturation Region:其他的ReLU他们没有Saturation Region,但是他有Saturation Region,不过ELU其实也有Saturation Region,因为SELU就只是ELU乘上一个λ而已;乘上这个λ有什么不同?乘上λ,让它在某些区域的斜率是大于1的,意味着说你进来一个比较小的变化,通过Region以后,他把你的变化放大1.0507700987倍,所以它的input能是会被放大的,而且这是他一个ELU的没有的特色。
8. Softmax激活函数
Softmax 是用于多类分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量,Softmax 可以将其压缩为长度为 K,值在(0,1)范围内,并且向量中元素的总和为 1 的实向量。
函数表达式如下: 𝑆𝑖=𝑒𝑖∑𝑗𝑒𝑗
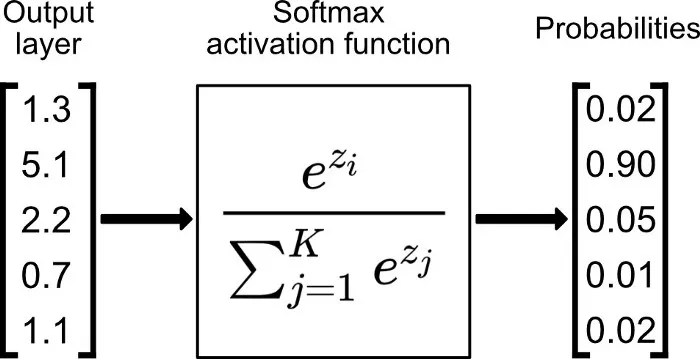
Softmax 与正常的 max 函数不同:max 函数仅输出最大值,但 Softmax 确保较小的值具有较小的概率,并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。
Softmax 函数的分母结合了原始输出值的所有因子,这意味着 Softmax 函数获得的各种概率彼此相关。
Softmax 激活函数的不足:
- 在零点不可微;
- 负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
9. Swish激活函数
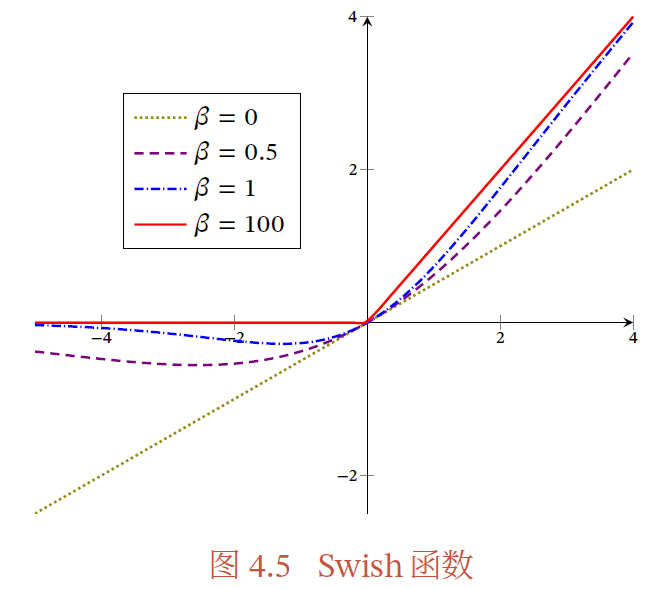
Swish激活函数又叫作自门控激活函数,它由谷歌的研究者发布,数学表达式为:
𝜎(𝑥)=𝑥∗𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝛽𝑥)=𝑥𝜎(𝛽𝑥)=𝑥1+𝑒−𝛽𝑥
𝛽 为可学习的参数或一个固定超参数, 𝜎(𝑥)∈(0,1) 可以看做是一种软性的门控机制。
当 𝜎(𝛽𝑥) 接近于1时,门处于“开”状态,激活函数的输出近似于x本身;
当 𝜎(𝛽𝑥) 接近于0时,门处于“关”状态,激活函数的输出近似于0;
当 𝛽=0 时,Swish 函数变成线性函数 𝑥/2 ;
当 𝛽=1 时,Swish 函数在 𝑥>0 时近似线性,在 𝑥<0 时近似饱和,同时具有一定的非单调性;
当 𝛽 趋于正无穷时, 𝜎(𝛽𝑥) 函数趋向于离散的0-1函数,Swish函数近似为ReLU函数;
因此,Swish 函数可以看作线性函数和ReLU 函数之间的非线性插值函数,其程度由参数 𝛽 控制。
10. Maxout激活函数
通常情况下,如果激活函数采用sigmoid函数的话,在前向传播过程中,隐含层节点的输出表达式为:
ℎ𝑖(𝑥)=sigmoid(𝑥⊤𝑊…𝑖+𝑏𝑖)
其中,一般情况下,W是2维的,这里表示的i是第i列,...表示的是对应第i列中的所有行。Maxout出现在ICML2013上,作者Goodfellow将maxout和dropout结合后,号称在MNIST, CIFAR-10, CIFAR-100, SVHN这4个数据上都取得了start-of-art的识别率。Sigmoid、ReLU等激活函数的输入是神经元的净输入z,是一个标量,而Maxout单元的输入是上一层神经元的全部原始输出,是一个向量x。这里如果采用maxout函数,表达式如下:
𝑓𝑖(𝑥)=max𝑗∈[1,𝑘]𝑧𝑖𝑗
𝑧𝑖𝑗=𝑥𝑇𝑊…𝑖𝑗+𝑏𝑖𝑗,𝑊∈𝑅𝑑×𝑚×𝑘
这里的W是3维的,尺寸为 dm k,其中d表示输入层节点的个数,m表示隐含层节点的个数,k表示每个隐含层节点对应了k个”隐隐含层”节点,这k个”隐隐含层”节点都是线性输出的,而maxout的每个节点就是取这k个”隐隐含层”节点输出值中最大的那个值。因为激发函数中有了max操作,所以整个maxout网络也是一种非线性的变换。因此当我们看到常规结构的神经网络时,如果它使用了maxout激发,则我们头脑中应该自动将这个”隐隐含层”节点加入。
Maxout 激活函数特点:maxout激活函数并不是一个固定的函数,不像Sigmod、Relu、Tanh等函数,是一个固定的函数方程。它是一个可学习的激活函数,因为我们 W 参数是学习变化的。Maxout单元不但是净输入到输出的非线性映射,而是整体学习输入到输出之间的非线性映射关系,可以看做任意凸函数的分段线性近似,并且在有限的点上是不可微的:
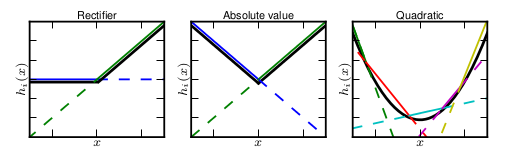
优点:Maxout的拟合能力非常强,可以拟合任意的凸函数。Maxout具有ReLU的所有优点,线性、不饱和性。同时没有ReLU的一些缺点。如:神经元的死亡。实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果。
缺点:从上面的激活函数公式中可以看出,每个神经元中有两组(w,b)参数,那么参数量就增加了一倍,这就导致了整体参数的数量激增。
11. Softplus激活函数
Softplus函数是Sigmoid函数原函数,即softplus函数求导的结果就是sigmoid函数。Softplus可以看做是ReLU函数的一个平滑版本,函数表达式如下:
𝑆𝑜𝑓𝑡𝑝𝑙𝑢𝑠(𝑥)=𝑓(𝑥)=log(1+𝑒𝑥)
𝑓′(𝑥)=𝑒𝑥1+𝑒𝑥 =11+𝑒−𝑥=𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝑥)
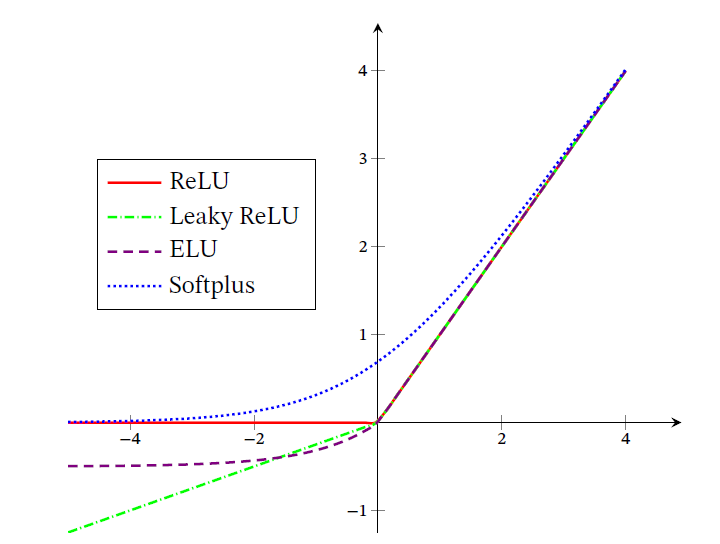
Softplus函数加了1是为了保证非负性。Softplus可以看作是强制非负校正函数max(0,x)平滑版本。红色的即为ReLU。
Softplus 函数其导数刚好是Logistic 函数.Softplus 函数虽然也具有单侧抑制、宽兴奋边界的特性,却没有稀疏激活性.
三、公式汇总