神经网络核心知识点梳理--一图了然
基于上篇文章的简单入门,这里重点梳理了一下神经网络的核心知识点,并以图片的方式呈现(点击放大哦~):
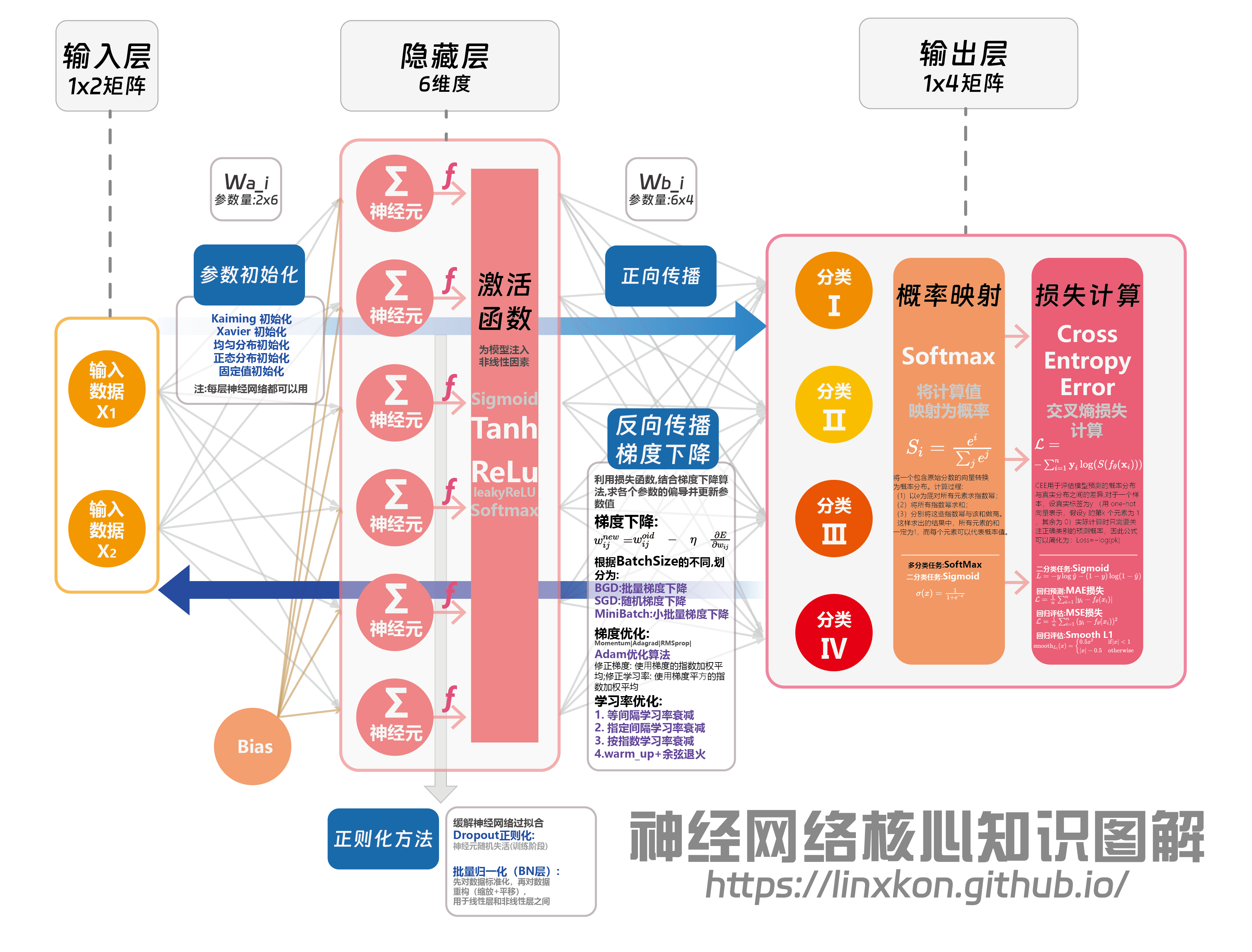
1.网络结构
1.1 输入层
- 1x2矩阵的输入数据X1和X2
- Bias(偏置)项作为额外输入,增强模型表达能力
1.2 隐藏层
- 6维度的神经元结构
- 每个神经元包含加权求和(Σ)和激活函数(f)
- 常用激活函数:
- Sigmoid: σ(x) = 1 / (1 + e^(-x))
- Tanh: tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
- ReLU: f(x) = max(0, x)
- Leaky ReLU: f(x) = max(αx, x), 其中α是小正数
1.3 输出层
- 1x4矩阵输出,对应4个分类
- 使用Softmax函数进行概率映射
- 交叉熵损失计算
1.4 权重矩阵
- Wa_i: 2x6维度,连接输入层和隐藏层
- Wb_i: 6x4维度,连接隐藏层和输出层
2.训练过程详解
2.1 前向传播
- 数据从输入层经过加权和激活,传递到输出层
- 隐藏层计算: H = f(X * Wa_i + b1)
- 输出层计算: Y = softmax(H * Wb_i + b2)
2.2 概率映射
- Softmax函数: Si = e^zi / Σ(e^zj)
- 将神经网络的原始输出转换为概率分布
- 确保输出和为1,便于多分类问题的概率解释
- 得出概率结果方便下一步概率计算
多分类问题使用softmax进行概率映射
二分类问题用sigmoid进行概率映射
2.3 损失计算
损失计算可以分为分类损失和回归损失两种,
多分类交叉熵损失(Cross Entropy Loss): L = -Σ(yi * log(ŷi)) 其中yi为真实标签,ŷi为预测概率
对于二分类问题,可使用二元交叉熵: L = -(y * log(ŷ) + (1-y) * log(1-ŷ))
损失函数用于量化模型预测与真实标签的差异,惩罚与真实标签差异大的
2.4 反向传播
- 计算损失函数对各层参数的梯度
- 使用链式法则逐层计算梯度
- ∂L/∂W = ∂L/∂Y * ∂Y/∂Z * ∂Z/∂W 其中Z为激活函数输入,W为权重
2.5 梯度下降
梯度下降相关概念:
- 正向传播+损失计算得出损失值来之后,我们希望找到损失函数取值最小的w(权重)
- 因损失函数皆为凸函数(碗的形状),即寻找令损失函数的导数为0的w
- 并不是所有损失函数都能直接求导找到这个点,所以我们通过反向传播+梯度下降的方式迭代去求该w
- 我们知道函数的导数方向(即梯度)是函数增长最快的方向,我们想要得到令损失函数导数为0的w,就要找到损失函数的负梯度方向
- 基于以上思路,假设我们当前的w是W_old,我们求此刻损失函数的偏导值,增加符号以得到它的负梯度方向,并乘以系数η控制其前进的步伐大小,得到 η * ∂L/∂W,再用W_old- η * ∂L/∂W得到W_new,新的w可以让损失函数的取值更小,以此类推,便可以通过多次迭代求得令损失函数取得最小值的w
综上,梯度下降的公式为:
W = W - η * ∂L/∂W
W:表示模型的参数(或权重),这些是我们希望优化的值。
η(学习率):这是一个超参数,控制每次更新步伐的大小。较大的学习率会导致更大的步伐,较小的学习率则会导致较小的步伐。选择合适的学习率非常重要,太大可能导致不稳定的收敛,太小可能导致收敛速度太慢。
L(损失函数):这是我们希望最小化的函数,它衡量了模型预测值与实际值之间的差距。
∂L/∂W(损失函数对参数的梯度):这是损失函数相对于参数的导数,表示了在当前参数值下,损失函数的变化率。通过计算这个梯度,我们可以知道如何调整参数 W来减少损失函数的值。
根据梯度下降时batchsize的不同,梯度下降的方法可以划分为
BGD批量梯度下降:全量样本all in训练,大型数据集基本不可行
SGD随机梯度下降:随机抽取单样本放入模型训练,受异常值影响,梯度更新时波动较大,训练时间长
MiniBatch小批量梯度下降:根据需求自由定义batchsize,兼具BGD和SGD的优点,收敛相对较快,最为常用
2.5.2梯度下降优化方法
在某些情况下(如线性回归),损失函数是凸函数,找到其导数为零的点可以找到全局最小值。但在更复杂的模型(如深度神经网络)中,损失函数通常是非凸的,导数为零的点不一定是全局最小值,也可能是鞍点(局部最优点)。因此,需要使用适当的优化算法来逼近最优解。
动量(Momentum):
v = γv - η * ∂L/∂W W = W + v γ为动量系数,通常取0.9
Adam优化器:
结合动量和自适应学习率 mt = β1mt-1 + (1-β1)gt vt = β2vt-1 + (1-β2)gt^2 W = W - η * mt / (sqrt(vt) + ε) 其中β1, β2为超参数,通常取0.9和0.999
2.6 正则化技术
- L1正则化: 添加|W|项到损失函数,促进稀疏性
- L2正则化: 添加||W||^2项,防止权重过大
- Dropout: 训练时随机"丢弃"一部分神经元,防止过拟合
- 批量归一化(Batch Normalization): 对每一层的输入进行标准化,加速训练收敛
3.高级训练技巧
3.1 参数初始化
- Xavier初始化: Var(W) = 1/nin
- Kaiming初始化: Var(W) = 2/nin (适用于ReLU激活)
- 均匀分布初始化
- 正态分布初始化
- 固定值初始化
3.2 学习率调整
- 学习率衰减: η = η0 / (1 + kt)
- 周期性学习率调整: Cosine Annealing
- 学习率预热(Warm-up): 从小学习率逐步增加到初始学习率
3.3 批量训练策略
- Mini-Batch: 平衡计算效率和梯度估计准确性
- 批大小选择: 较大批量可提高并行度,但可能影响泛化性
3.4 进阶优化策略
- 梯度裁剪: 防止梯度爆炸
- 学习率自适应: 如Adagrad、RMSprop等算法
- 早停(Early Stopping): 监控验证集性能,及时停止训练防止过拟合
深入理解神经网络的结构、训练过程和优化技巧,对于构建高效且性能优异的模型至关重要。从基础的前向传播、损失计算,到复杂的优化算法和正则化技术,每个环节都在平衡模型的拟合能力和泛化性能。通过合理运用这些技术,我们可以训练出既能准确拟合训练数据,又具有良好泛化能力的神经网络模型。