选择RLHF还是SFT

随着 [Llama3] 的开源，人们对 Alignment 的重视程度又上一个阶梯。作为 Alignment 家族中的核中核，RLHF 家族也开始变的繁荣昌盛，这对各位 RLer 来说可真是喜闻乐见。今天我们就一起来俯瞰一下当下 RLHF 都有些什么奇巧的魔改思路。如果你还不太清楚 RLHF 的一些基本概念，可以试着看看这篇文章：何枝：【RLHF】RL 究竟是如何与 LLM 做结合的？

如今，LLM 中主流 RLHF 方向分为两大路线：

以 [PPO] 为代表的 On Policy 路线
以 [DPO] 为代表的 Off Policy 路线

那究竟什么是 On Policy，什么是 Off Policy 呢？

我们可以简单理解为：凡是需要 LLM 在训练过程中做 generation 的方法就是 On Policy，反之为 Off Policy。

我们通常会说 On Policy 的方法会更耗卡、训练更耗时，这里的「耗时」主要就体现在模型做「生成」上。

想想看，我们做 SFT 的时候只用给定训练训练数据，模型做一遍 forward 就能算出 loss，然后更新。

但如果训练过程中加入了「模型生成答案」这个环节，那耗时可就长多了，

毕竟对于生成任务而言，模型需要一个 token 一个 token 依次生成，可不慢吗。

不过，虽然慢了些，On Policy 的方法相较于 Off Policy 方法理论有着更高的效果上限，这点我们将在后面分析。

1. On Policy 路线

前面我们提到了，On Policy 的核心思路就是：让模型自己做生成，我们根据模型生成结果的好坏来打分，用于指导模型进行更新。

这里最关键的点是：让模型尝试「自己生成答案」，为什么说这一点很关键呢？

想象一下，如果今天你是一个被训练的模型，你的任务是学会玩王者荣耀。

那么现在有两种训练你的方法：

第一种：有一个教练在你旁边，你操作的时候他就在旁边对你的每一个操作给予评价。当你推掉一座塔时，教练夸你很有天赋，当你因为上头结果被对面反杀时，他提醒你下次吸取教训。
第二种：不直接让你玩游戏，而是给你一堆职业选手比赛的录像，还有一堆青铜玩家的对局，告诉你职业选手的操作是好的，青铜玩家的操作是不好的，你应该多学习职业玩家的操作，避免青铜玩家的操作。

宇宙免责声明：上述内容仅为例子，不歧视任何青铜玩家，我也青铜水平。

看出来了吗，这两种方法最大的区别就在于：你有没有亲自下场去「玩游戏」。

对于第二种而言，尽管你能看到什么是「好操作」，什么是「坏操作」，但并不是真的每一个操作对你都有帮助。

比如，就算你知道职业选手的操作是好操作，你也打不出来（对你来说太难了）；

而青铜玩家的操作，就算不看它你也不会打出那么生疏的操作。

上述两种方法中的「第一种」就是 On Policy 的方法，即需要模型亲自输出答案，然后根据反馈学习；

「第二种」即为 Off Policy 的方法，模型不需要亲自输出答案，根据给定的「好坏样本」来进行模拟学习。

由此我们可以看出，Off Policy 的训练速度能够更快（只用看大量的样本来学习，不用亲自去玩），但非常依赖给定的数据是否和「模型自身能力」足够相近。最理想的效果就是，找到大量和你自身水平差不多的玩家的对局资料给你学习，这些训练样本的利用率才是最高的。

反之，对于 On Policy 而言就不用担心「训练样本是否匹配」的问题，

毕竟所有的训练样本都是当前模型自己吭哧吭哧生成的，百分之百的匹配！

下面，我们就来看看一个完整的 On Policy 的算法都需要哪些组成部分：

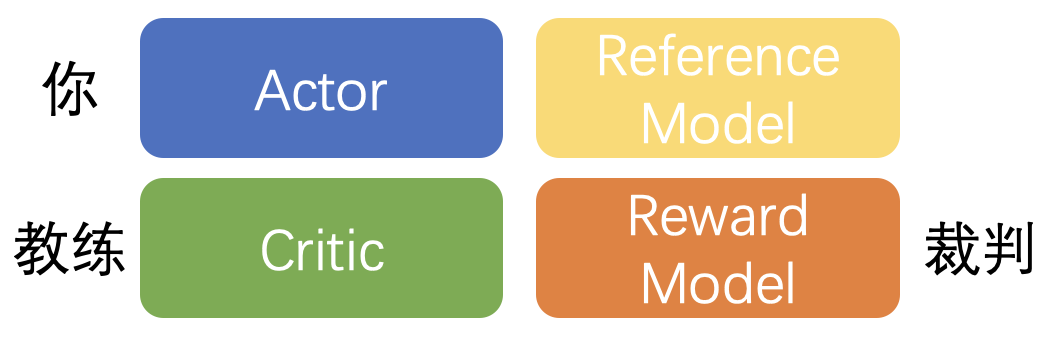
PPO 训练所需要的 4 个模型，通常情况下 4 个模型是一样规模大小的 LLM

上图是一个标准 PPO 所需要的 4 个模型，其中：

Actor：用于生成句子的模型，也就是正在被训练玩游戏的你。
Critic：指导你进步的教练模型，注意，这个教练模型也会随着你的进步来调整自己的指导策略。比如，当你很菜的时候，突然打出了一个很强的操作时，会给你一个较高的分数（Vs 较低，因此 r - Vs 就较大，看不懂这句话没关系，我只是尝试证明这个例子的存在一定合理性），当你本身比较强了，再打出同样操作的时候给的奖励就没有之前那么高。因此，训练过程中 Critic 是和 Actor 一起训练的。
Reward Model：用于给出最终分数的模型。虽然教练能够给你一定的指导，但最终游戏获胜与否还是要靠裁判说了算，可以说教练在教你的同时也在尝试学习裁判的偏好。裁判一般是固定的，因此 Reward Model 在整个训练过程中参数是被冻结的。
Reference Model：这是 PPO 在 LLM 中独有的概念，目的是为了让 actor 不要训练偏离太远，主要是缓解 reward hacking + 稳定训练使用的。

通常来讲，这 4 个模型都是同样规模参数的模型，

也就是说，如果我们选用 llama3-70B 作为训练模型的话，整个训练过程中我们需要同时载入 70 x 4 = 280B 的参数，这当中有 70 x 2 = 140B 的参数需要进行训练，这就是为什么 PPO 非常耗卡的原因。

于是，针对 PPO 耗卡且训练慢的特点，就涌现出一系列的工作尝试解决该问题。

1.1 ReMax

[ReMax] 认为，我们可以丢掉 Critic（教练），Actor 不再需要受到 Critic 的指导，而是直接去对齐 RM（裁判），

这样一来，我们就只用载入 3 个模型，3 x 70 = 210B，并且只有 70B 的参数在学习（省了一半）。

其实，在 PPO 之前，最早是没有 Critic 的（Policy Gradient，我在上一篇文章有讲到），

我们只让 actor 去生成行为，然后利用所有行为共同获得分数来训练模型，

但是，因为每一个行为（对应生成句子中的每一个 token）都是一个随机变量，

N 个随机变量加在一起，方差就会非常巨大，这通常会导致整个 RL 训练崩掉。

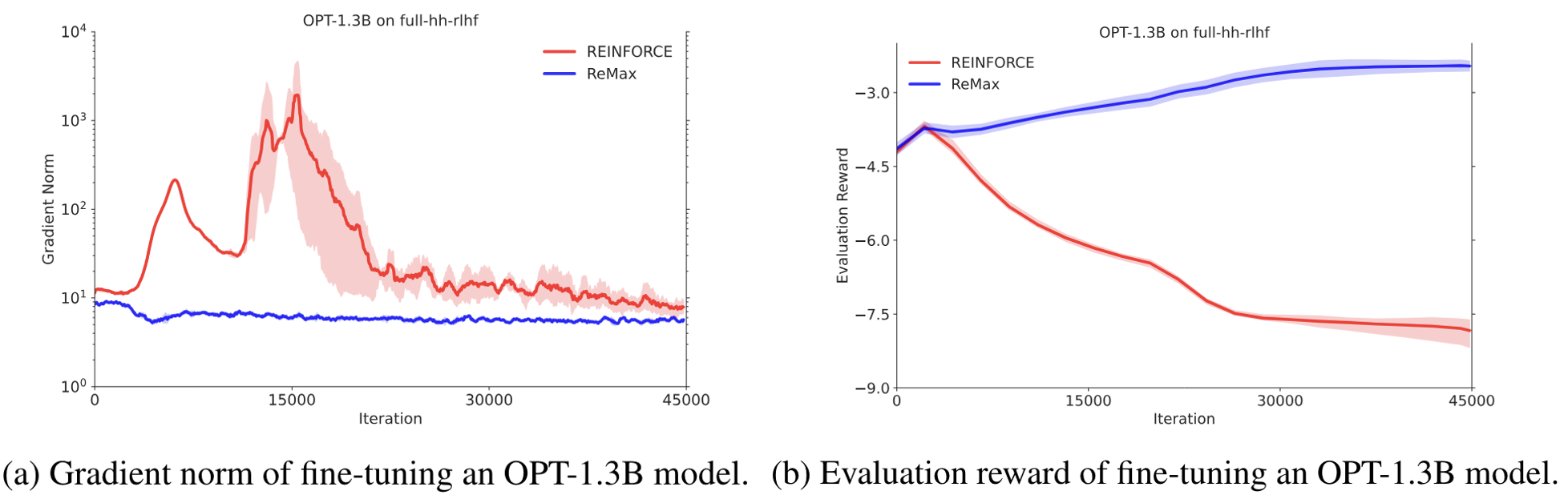
Remax 中给的例子，图中的 REINFROCE 即为 N 个随机变量直接相加的方法

从上述图中可以看到：

图左红线是随机变量直接叠加的方法，训练时梯度方差特别大，

对应到图右，训练没几步 reward 就开始崩溃，预示着训练失败。

为了解决这个问题，我们可以让每一个随机变量都减掉一个 baseline，这样就可以降低方差，稳定训练。

那么这个 baseline 如何得到呢？

一种很直觉的想法是：我们随机采样 N 次，将这 N 次采样结果的得分「求均值」并作为 baseline，

但这个方法的缺陷也很明显，只有当 N 足够大时，方差才能足够小。

对此，PPO 的处理方式是：使用一个神经网络 Critic 去拟合这个均值（而不是直接叠加），从而减小方差。

而 ReMax 的思路就比较有趣：使用「当前策略」认为最好的行为来当作 baseline 值。

ReMax 计算 gradient 的函数

可以看到，在 PPO 中我们计算 actor 分数时是： r−V(s)r - V(s)r - V(s) ，而在 ReMax 中变成了： r−rgreedyr - r_{greedy}r - r_{greedy} 。

其中，r(greedy) 是指对于一个 prompt，LLM 在 greedy sample 的情况下生成一个句子，该句子的得分。

PS：通常情况下我们在 On Policy 训练过程中，LLM 在做 generate 的时会采用 top_p = 1.0, top_k = -1 的采样方式，以增强模型的探索。

使用 greedy 策略生成句子的得分做为 basline，这之所以能够降低方差，

是默认认为通常 SFT 模型已经经过一部分对齐，对于同一个 prompt 模型不太会输出差异性过大的答案。

这样看来，ReMax 优化思路也很直觉：模型每次只需要和当前 greedy 策略下进行比较，当这次「探索」的句子的得分大于 greedy 策略生成的句子，那么就鼓励模型朝着这次探索的句子分布进化。于是，很有可能在下一次 greedy 采样时，当前被探索出来的优秀答案就能被采出。

除此之外，ReMax 最大的优势是在于：它丢掉了一个巨大的 Critic 网络。

因此，在只有 4 张 A800-80G 的情况下，ReMax 也能在不使用 offload 的情况下训练 [Llama-7B]。

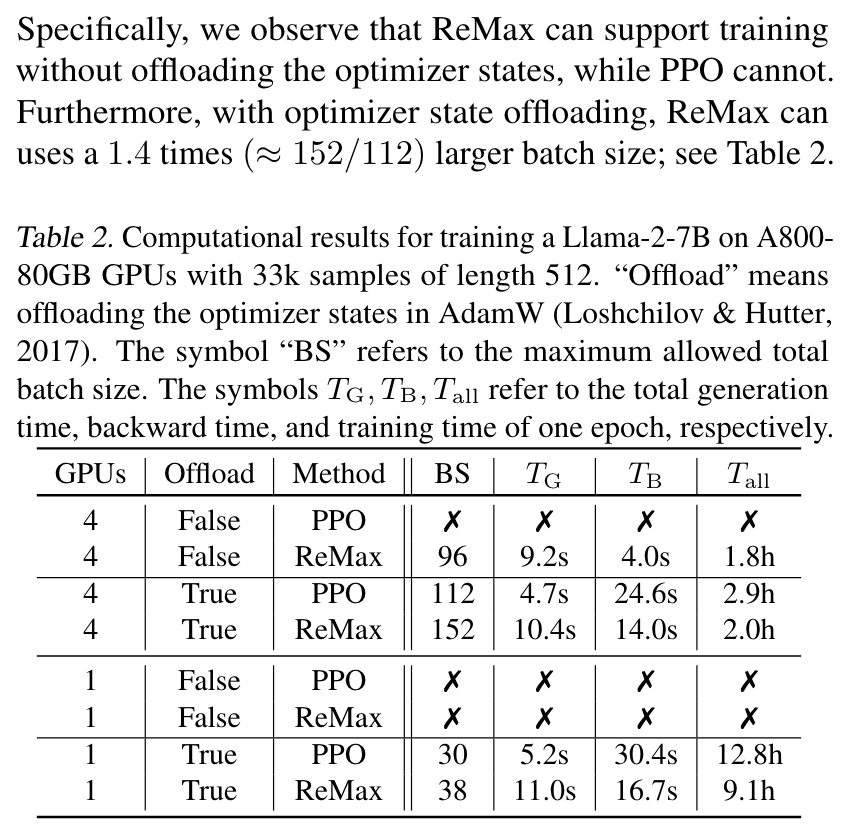
PPO v.s. ReMax，在 4 卡不使用 offload 时，PPO 跑不起来，ReMax 可以，并且 ReMax 不用更新 Critic，backward 也能更快一些

训练一步的时间对比如下：

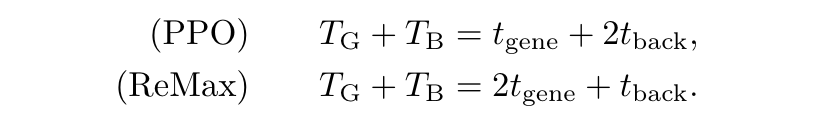
PPO v.s. ReMax 单步训练时间

PPO 只用做一次 generation，需要更新 2 次参数（actor + critic）；

ReMax 需要做两次 generation（训练 sample 1 次 + greedy sample 1 次），需要更新 1 次参数（actor）。

PS：论文中讨论的 PPO 是 actor 和 critic 串行 backward 的情况，事实上由于 actor 和 critic 的 loss 是没有相互依赖的，通常我们可以做成异步更新，其实也就只有 1 个 t_back。

[源码] 中计算 loss 的部分如下：

def compute_loss(self, inputs):
    prompts = inputs["prompts"]
    log_probs = inputs["logprobs"]
    ref_log_probs = inputs["ref_logprobs"]
    reward_score = inputs["rewards"]
    baseline_reward_score = inputs["baseline_rewards"]
    attention_mask = inputs["attention_mask"]
    seq = inputs["input_ids"]

    start = prompts.size()[-1] - 1
    action_mask = attention_mask[:, 1:]

    with torch.no_grad():
        kl_divergence = -(log_probs - ref_log_probs)
        kl_divergence = self.kl_ctl * kl_divergence

        reward_score = reward_score - baseline_reward_score         # 真实 reward
        returns, kl_ratio = self.compute_returns(
            prompts, kl_divergence, reward_score, action_mask
        )

    # process the new outputs
    batch = {"input_ids": seq, "attention_mask": attention_mask}
    logits = self.actor_model(**batch, use_cache=False).logits
    log_probs = gather_log_probs(logits[:, :-1, :], seq[:, 1:])

    actor_loss = self.actor_loss_fn(
        log_probs[:, start:], returns[:, start:], action_mask[:, start:]
    )
    return actor_loss, returns[:, start:], kl_ratio


# reward & basline_reward_score 计算如下:
seq = self._generate_sequence(
    self.actor_model,
    prompts,
    ...
)
baseline_seq = self._generate_sequence(
    self.actor_model,
    prompts,
    ...
    do_sample=False,
)
reward_score = self.reward_model.forward_value(
    seq, action_mask, prompt_length=self.prompt_length
)
baseline_reward_score = self.reward_model.forward_value(
    baseline_seq, baseline_action_mask, prompt_length=self.prompt_length
)

1.2 Group Relative Policy Optimization(GRPO)

在 ReMax 中我们提到：使用一种好的方法来计算 baseline 是丢掉 Critic 网络的关键。

在 [DeepSpeek-v2] 的 RLHF 过程中，这个思路也有被使用，

不过计算 baseline 的方式稍有不同，文章中将其称为 [GRPO]。

GRPO 认为，直接退化为 Policy Gradient 是不是有点过于原始，

虽然天下苦 Critic 久矣，PPO 中其他先进 features 咱们还是可以保留的：比如 importance sampling 和 clip。

于是，整个优化目标就变成这样：

GRPO 的优化目标（绿色部分）和 PPO 几乎完全一样（只是 Advantage 的计算方式变了）

上图中绿色部分是不是非常眼熟，这不就是 PPO 的优化目标嘛。

但现在的问题是：公式中的 AiA_iA_i 在 PPO 中是需要通过 Critic 去参与计算的（ r+Vsnext−Vsr + V_{s_{next}} - V_{s}r + V_{s_{next}} - V_{s} ），可是GRPO 里没有 Critic 啊，这咋计算！

我们回想一下：Critic 的目标是去估计一个状态的期望值（从而降低方差），而期望的近义词是均值，

那我们直接暴力的去采样 N 次求均值来代替这个期望不就好了！

没错，这就是 GRPO 暴力且有效的方法：

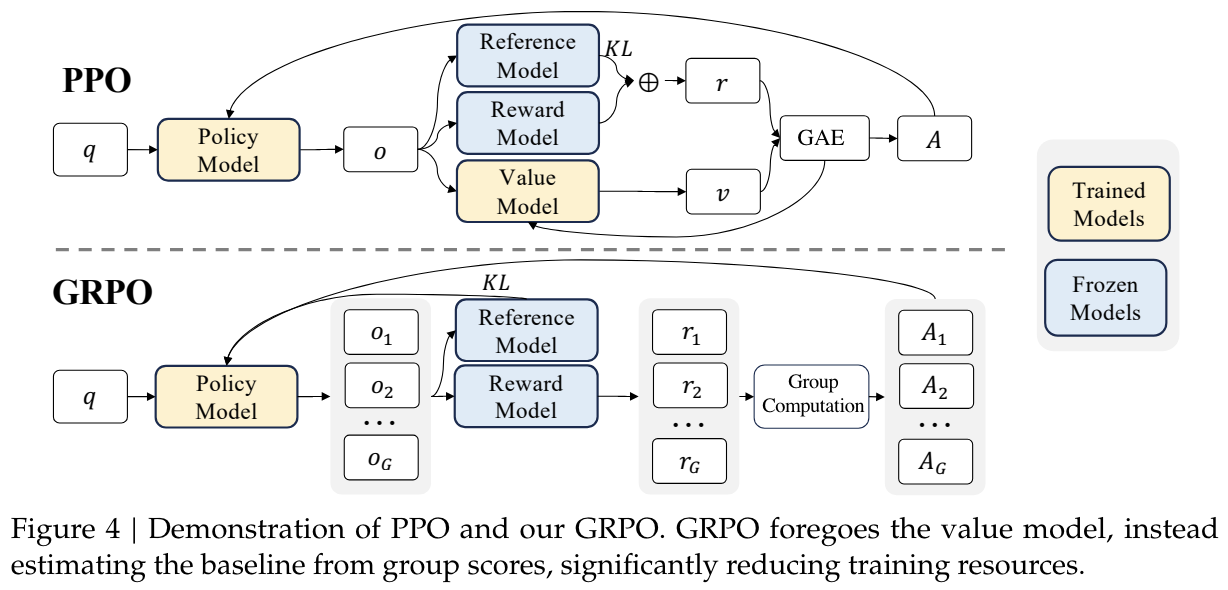
PPO v.s. GRPO，对于同一个 prompt 采 G 个答案，平均 G 个答案的得分当作 baseline

这里有几个值得注意的细节：

GRPO 中也加入了 KL Penalty，只不过不像 PPO 的实现是每个 token 位置上加一个惩罚，而是直接一并计算完后加到最后的 loss 中去。
KL Penalty 使用 [Schulman 近似值] 用以保证 KL 始终为正数，即： ratio−1−logratioratio - 1 - logratioratio - 1 - logratio 。
句子的最终得分为： Ai=ri−mean(r)std(r)A_i = A_i = ，由于在 LLM 里我们通常将 GAE 中的 γ设置为 1.0，因此在这里 GRPO 也直接将这个最终得分复制到句子中的每一个 token 上进行训练。

尽管这种方法确实可以省掉一个 Critic，但成功需要具备 2 个关键：

SFT 对给定的 prompt 不能有着太 diverse 的输出，否则方差会比较大。
对同一个 prmopt 采样的数量要可能大，这样才能降低方差。

我推测这可能是论文选择在「数学任务」上使用这种方式进行训练的原因。

2. Offline 路线

尽管人们一直在尝试使用各种方法来降低训练门槛， Online 的方法依然有着不小的资源 & 人力需求量，

就算砍掉一个 Critic，至少还需要 Actor & Reference & Reward Model 3 个模型。

有没有什么办法我们只使用 1 个模型就能完成 RLHF，就和 SFT 训练一样呢？

还真有。

还记得最早我们举的「学王者荣耀」的例子吗，有一种训练方法是：

不用你亲自下场玩游戏，而是给你一堆「好操作」和「坏操作」的视频给你，你从里面尽可能的去学习「好操作」，避免「坏操作」。这种通过看别人的操作学习，既不需要教练（Critic），也不需要裁判（Reward Model），只需要你一个人（Actor）自己看就行了，这不就剩资源了吗。

2.1 Direct Preference Optimization（DPO）

[DPO] 就是第一个使用这种方法来进行 RLHF 的算法，

其思路很直觉：对于同一个 propmt，给定一个好的回答 ywy_wy_w 和一个不好的回答 yly_ly_l，通过降低不好回答被采样的概率，提升好回答的概率，从而进行模型训练。这个数据和训练 Reward Model 的 pair 数据格式完全一致，都是同一个 prompt 对应两个不同质量的 responses。

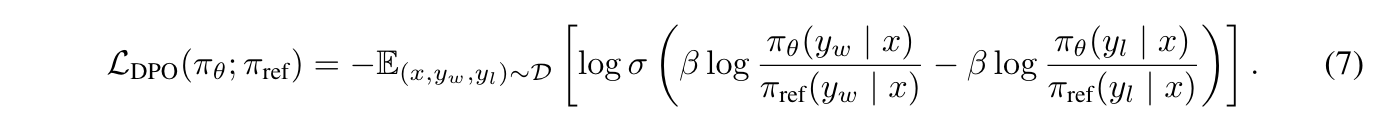
DPO 的 loss function

[源码] 中计算 loss 的部分：

def dpo_loss(
        self,
        policy_chosen_logps,
        policy_rejected_logps,
        reference_chosen_logps,
        reference_rejected_logps,
    ):
        """Compute the DPO loss for a batch of policy and reference model log probabilities.

        Args:
            policy_chosen_logps: Log probabilities of the policy model for the chosen responses. Shape: (batch_size,)
            policy_rejected_logps: Log probabilities of the policy model for the rejected responses. Shape: (batch_size,)
            reference_chosen_logps: Log probabilities of the reference model for the chosen responses. Shape: (batch_size,)
            reference_rejected_logps: Log probabilities of the reference model for the rejected responses. Shape: (batch_size,)
        """
        pi_logratios = policy_chosen_logps - policy_rejected_logps
        ref_logratios = reference_chosen_logps - reference_rejected_logps

        pi_logratios = pi_logratios.to(self.accelerator.device)
        ref_logratios = ref_logratios.to(self.accelerator.device)
        logits = pi_logratios - ref_logratios

        losses = -F.logsigmoid(self.beta * logits)
        return losses

2.2 Fixing Failure Modes of Preference Optimisation with DPO-Positive（DPOP）

DPO 有一个非常致命的问题，

由于 DPO 的训练 loss 目标是「尽可能最大化好答案和坏答案之间的采样概率差」，

一种常见的情况是：好答案 & 坏答案被采样的概率同时在变低，只不过坏答案降低的比好答案更多。

这样一来，虽然好坏答案之间的概率差变大了，但这个过程中「好答案」被采样的概率也降低了，

这并不是我们想要的！

这种情况在 chosen 和 rejected 答案有大部分内容相同，仅有少部分内容不同时较为常见。

好答案 / 坏答案只差了一个 token，但是作为坏的答案，then 之后的正确部分在 DPO 训练过程中也将被降低采样概率

为此，[DPOP] 在 DPO loss 的基础上加入了一个正则项：

若当前 chosen 答案在 SFT 模型中采样概率 > 当前 Policy 模型的采样概率，则减去一个正则化系数（当前的 chosen 答案 policy 还没有拟好，别再更新那么猛了）；
若当前 chosen 答案在 Policy 模型中采样概率更高，证明 Policy 已经对这个 chosen 答案拟合的比较充分了，此时着重降低一下坏答案的采样概率。

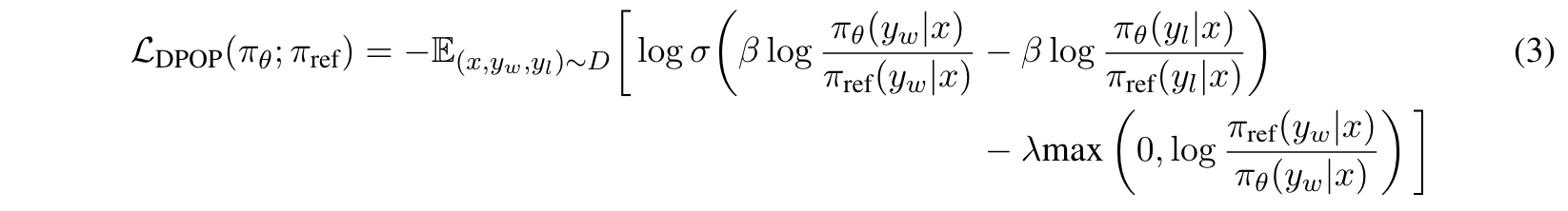
DPOP loss function，尾巴上添加一个正则化项

使用这种方法，相当于在「好答案」和「坏答案」中添加了一个截断式的 “attention”，让模型优先学会 chosen 答案，当对好答案学的足够好时再着重考虑惩罚坏答案，从而降低 DPO 模型 “训崩” 的可能性，最起码也要不弱于单拿 chosen 数据出来做 SFT 的效果。

2.3 Token-level Direct Preference Optimization（TDPO）

在 PPO 训练的时候，我们通常会加上 KL 惩罚来约束模型不要偏离 reference model 过远，

但在 DPO 的实现中却没有并没有添加这一项。

[TDPO] 提出了这一改进，在原来的 DPO loss 上新增了 kl 惩罚项：

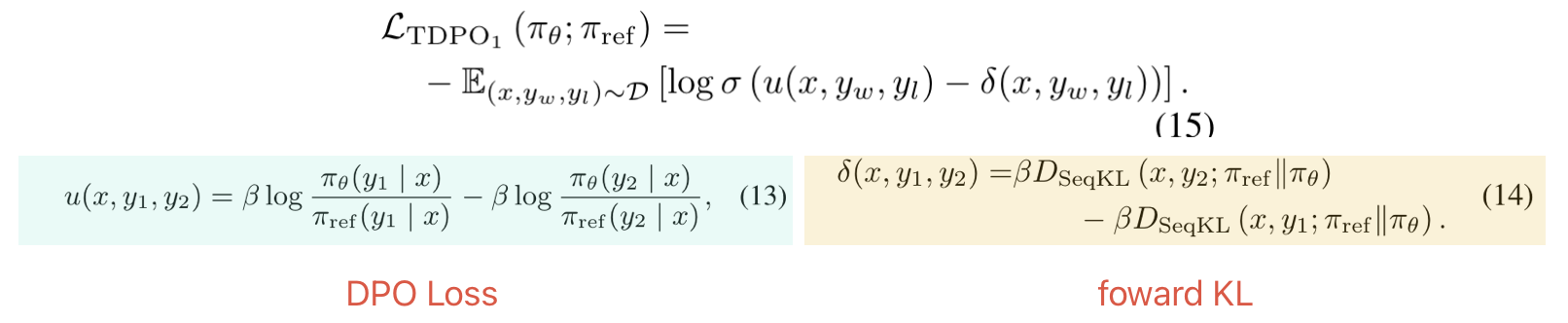
TDPO loss function，在尾部加了一个 KL 惩罚

不过，不同于 PPO 中使用 backward KL，TDPO 则是使用 forward KL 来计算 KL 惩罚，

因为 KL 是一个非对称的距离函数，所谓 forward 和 backward 其意思就是「以 SFT 计算采样概率」还是「以 Policy Model 计算采样概率」。

在 [源码] 中我们能更直观的看到 forward KL 的计算方式：

vocab_logps = logits.log_softmax(-1)

reference_vocab_ps = reference_logits.softmax(-1)
reference_vocab_logps = reference_vocab_ps.log()

# forward kl 计算
# backward kl (PPO) 应为: vocab_logps - reference_vocab_logps
per_position_kl = (reference_vocab_ps * (reference_vocab_logps - vocab_logps)).sum(-1)
per_token_logps = torch.gather(vocab_logps, dim=2, index=labels.unsqueeze(2)).squeeze(2)
per_reference_token_logps = torch.gather(reference_vocab_logps, dim=2, index=labels.unsqueeze(2)).squeeze(2)

由于 backward KL 的目标是拟合整个分布中的「一部分」，而 forward KL 的目标是尽可能 cover 整个分布中的大部分。因此，TDPO 训练后的模型会比 PPO 训练后的模型，在输出多样性上更加自由。

PS：经过 PPO 后的模型基本一眼就能看出来，输出风格都非常一致，因为此时输出分布已经「聚集」到一个局部分布上了，reward 方差会比 SFT 小很多。

完成 loss 函数如下：

def tdpo_loss(
        chosen_logps_margin,
        rejected_logps_margin,
        chosen_position_kl,
        rejected_position_kl,
        beta: float, 
        alpha: float = 0.5, 
        if_tdpo2: bool = True
    ):
    """Compute the TDPO loss for a batch of policy and reference model log probabilities.

    Args:
        chosen_logps_margin: The difference of log probabilities between the policy model and the reference model for the chosen responses. Shape: (batch_size,)
        rejected_logps_margin: The difference of log probabilities between the policy model and the reference model for the rejected responses. Shape: (batch_size,)
        chosen_position_kl: The difference of sequential kl divergence between the policy model and the reference model for the chosen responses. Shape: (batch_size,)
        rejected_position_kl: The difference of sequential kl divergence between the policy model and the reference model for the rejected responses. Shape: (batch_size,)
        beta: Temperature parameter for the TDPO loss, typically something in the range of 0.1 to 0.5. We ignore the reference model as beta -> 0.
        alpha: Temperature parameter for the TDPO loss, used to adjust the impact of sequential kl divergence.
        if_tdpo2: Determine whether to use method TDPO2, default is True; if False, then use method TDPO1.
    """
    chosen_values = chosen_logps_margin + chosen_position_kl
    rejected_values = rejected_logps_margin + rejected_position_kl
    chosen_rejected_logps_margin = chosen_logps_margin - rejected_logps_margin

    if not if_tdpo2:
        logits = chosen_rejected_logps_margin - (rejected_position_kl - chosen_position_kl)    # tdpo1
    else:
        logits = chosen_rejected_logps_margin - alpha * (rejected_position_kl - chosen_position_kl.detach())  # tdpo2
    losses = -F.logsigmoid(beta * logits)

    chosen_rewards = beta * chosen_values.detach()
    rejected_rewards = beta * rejected_values.detach()

    return losses, chosen_rewards, rejected_rewards

2.4 Monolithic Preference Optimization without Reference Model（ORPO）

上述一系列类 DPO 的方法已经将 RLHF 的训练成本从 4 个模型砍到 2 个，

在这种情况下，咱们还能再省吗？

当然！说到省，现在天猫 618...想多了，我接不到广告。

不管是哪种 DPO，除了 policy model 外，都还有一个 reference model，我们能不能把 ref_model 也干掉。

回想一下，在 DPOP 中，我们使用 ref_model 来保证模型在 chosen 上的概率不要过低，

如果只是为了保证模型能够拟合 chosen 答案，那我们是不是直接把 chosen 答案拿出来做 SFT 就好，

这不就不需要 ref_model 来吗？

[ORPO] 的目标函数一共由两部分组成（SFT Loss + Odds Ratio Loss）：

ORPO 的 loss function

其中 SFT Loss 就是拿 chosen 答案算 CrossEntropy Loss，这很好理解，剩下的就是这个 Odds Ratio 是什么。

在统计学和概率论中，odds 指的是「某事件发生与不发生的比例」，

比如，如果一件事情发生的概率是 ppp，那么它不发生的概率就是 1−p1 - p1 - p，其 odds 计算公式就为：

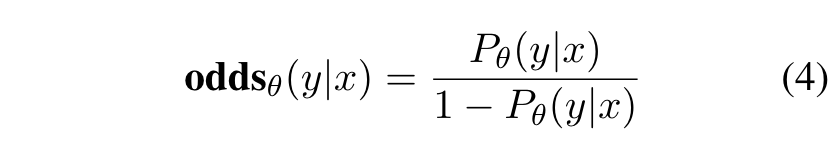
odds 值的计算公式

当一件事情的发生概率越大，其对应的 odds 值就越大。

知道 odds 的概念后，我们再一起上述 loss function 的后半部分 LORL_{OR}L_{OR} 的定义：

式子中上半部分为「好样本」发生的 odds 值，下半部分为「坏样本」发生的 odds 值

通过 minimize 这个 loss 值，我们就需要 maximize 括号内的值，也就是尽可能的让「好句子」发生的概率增大，「坏句子」发生的概率减小。

由此可见，ORPO 通过定义了一个神奇的 odds 值来提升好样本的概率，降低坏样本的概率，并通过一个 SFT loss 来保证模型对 chosen response 的基本拟合。

[源码] 中对 odds_ratio 的计算如下：

def odds_ratio_loss(
        self,
        policy_chosen_logps,
        policy_rejected_logps,
    ):
        """Compute ORPO's odds ratio (OR) loss for a batch of policy and reference model log probabilities.

        Args:
            policy_chosen_logps: Log probabilities of the policy model for the chosen responses. Shape: (batch_size,)
            policy_rejected_logps: Log probabilities of the policy model for the rejected responses. Shape: (batch_size,)

        Returns:
            A tuple of three tensors: (losses, chosen_rewards, rejected_rewards).
            The losses tensor contains the ORPO loss for each example in the batch.
            The chosen_rewards and rejected_rewards tensors contain the rewards for the chosen and rejected responses, respectively.
            The log odds ratio of the chosen responses over the rejected responses ratio for logging purposes.
            The `log(sigmoid(log_odds_chosen))` for logging purposes.
        """
        # Derived from Eqs. (4) and (7) from https://arxiv.org/abs/2403.07691 by using 
        # log identities and exp(log(P(y|x)) = P(y|x)
        log_odds = (
            policy_chosen_logps - policy_rejected_logps
            ) - (
            torch.log1p(-torch.exp(policy_chosen_logps)) - 
            torch.log1p(-torch.exp(policy_rejected_logps))
        )
        sig_ratio = F.sigmoid(log_odds)
        ratio = torch.log(sig_ratio)
        losses = self.beta * ratio
        return losses

好啦，以上就是一些对 RLHF 的介绍啦，其实不管 On Policy 还是 Off Policy，找到适合自己场景的方法才是最重要的，很开心能看到如今百花争鸣的繁荣景象，希望未来会越来越好。

RLHF

#LLM #模型训练

选择RLHF还是SFT

https://linxkon.github.io/选择RLHF还是SFT.html

作者

linxkon

发布于

2024年10月1日

许可协议

AI Agent：多模态交互前沿调查-李飞飞团队上一篇

RAG中的rerank技术下一篇